Formula de calcul a diagonalei unui romb

Un romb este un patrulater cu patru laturi egale, un patrulater cu două diagonale perpendiculare unul pe celălalt la mijlocul fiecărei drepte este un romb, un paralelogram cu două laturi adiacente egale... Pe lângă pătrate, dreptunghiuri, triunghiuri... rombul este una dintre formele importante din matematică și viață.

Pe lângă formula de calcul a perimetrului și a ariei unui romb , este foarte importantă modalitatea de calculare a diagonalei unui romb - linia care leagă vârfurile opuse ale rombului.

Articolul de mai jos vă va ajuta să învățați cum să calculați diagonala unui romb cu exemple specifice, vă rugăm să consultați el.

Cuprins

• Diagonala unui romb
• Proprietățile diagonalelor unui romb
• Formula de calcul a diagonalei unui romb
• Problemă la calcularea diagonalei rombului

Diagonala unui romb

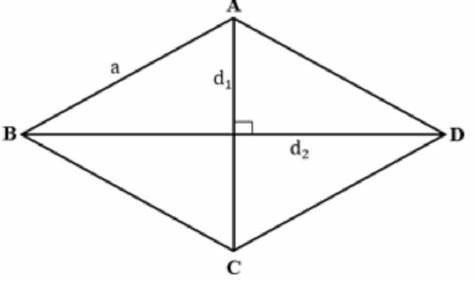
• Diagonala unui romb este linia care leagă două vârfuri opuse ale rombului.
• Un romb are două diagonale și se intersectează la mijlocul rombului.
• Diagonala împarte rombul în două triunghiuri echilaterale cu laturile egale.

Proprietățile diagonalelor unui romb

Cele două diagonale dintr-un romb au următoarele proprietăți:

• Două diagonale egale: Cele două diagonale ale unui romb sunt de lungime egală.
• Unghiul dintre două diagonale este un unghi drept: cele două diagonale ale unui romb se intersectează la mijlocul rombului și formează un unghi drept.
• Diagonalele sunt axele de simetrie ale unui romb: Fiecare diagonală a unui romb este o axă de simetrie a rombului, împărțind rombul în două jumătăți simetrice.
• Diagonalele sunt diagonale a două triunghiuri echilaterale: Fiecare diagonală a unui romb este o diagonală a două triunghiuri echilaterale, formate din laturi egale.
• Produsul lungimilor celor două diagonale este egal cu produsul lungimilor celor două laturi ale unui romb: Produsul lungimilor celor două diagonale este egal cu produsul lungimilor celor două laturi ale unui romb. Adică, dacă notăm diagonala cu d, iar laturile cu a și b, avem d² = a² + b².

Aceste proprietăți sunt proprietăți caracteristice romburilor și sunt utilizate în multe probleme geometrice care implică romburi.

Formula de calcul a diagonalei unui romb

Vă rugăm să luați în considerare exemplul de mai jos pentru a obține formula de calcul a diagonalei unui romb.

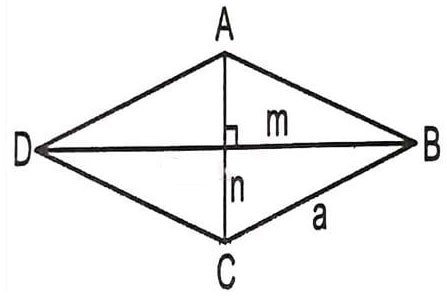
Să presupunem că trebuie să calculăm lungimea diagonalei unui romb ABCD cu latura a și un unghi ABC = 60 de grade -> care este formula de calcul a diagonalei unui romb în acest caz?

Soluţie:

Deoarece ABCD este un romb, toate laturile sunt egale cu a.

Considerăm triunghiul ABC cu: AB = BC = a

Din nou: ABC = 60 de grade => Triunghiul ABC este un triunghi echilateral cu latura a.

=> AB = AC = BC = a

=> Lungimea diagonalei rombului este AC = BD = a.

Soluția de mai sus este una dintre cele mai simple și mai ușor de înțeles formule pentru calcularea diagonalei unui romb.

Formula de calcul a diagonalei unui romb la cunoașterea ariei și a diagonalei rămase

Din formula pentru calcularea ariei unui romb:

S = (axb): 2

Avem formula pentru lungimea diagonalei după cum urmează:

a = S x 2 : b

sau

b = S x 2 : a

Acolo:

• S este zona
• a și b sunt lungimile celor două diagonale

Utilizați proprietățile geometrice ale unui romb pentru a calcula lungimea diagonalei fără a utiliza teorema lui Pitagora. Mai exact:

Diagonala unui romb este media celor două înălțimi.

Diagonală = rădăcină pătrată a (înălțime lungă + înălțime scurtă)²

Diagonala unui romb este jumătate din perimetrul rombului.

Diagonala = 1/2 x perimetrul rombului.

Problemă la calcularea diagonalei rombului

Problema 1: Având în vedere un romb cu o suprafață de 360 ​​de centimetri pătrați și o lungime a diagonalei de 24 de centimetri. Calculați lungimea celei de-a doua diagonale

Soluţie:

Conform formulei pentru aria unui romb: axb : 2

Avem a doua diagonală: 360 x 2 : 24 = 30cm

Raspuns: 30 cm

Problema 2:

Un romb are o suprafață de 4 dm, lungimea unei diagonale este de 3/5 dm. Calculați lungimea celei de-a doua diagonale. Soluţie:

Lungimea celei de-a doua diagonale este:

(4 x 2) : 3/5 =40/3 (dm)

Lecția 3: Cele două diagonale ale unui romb au lungimi de 160cm și 120cm. Calculați înălțimea rombului, știind că raportul dintre înălțimea și lungimea laturii rombului este 24:25.

Soluţie:

Aria rombului este: 160.120:2 = 9 600 (cm2).

Deoarece raportul dintre înălțimea și lungimea laturii unui romb este 24:25, putem considera că înălțimea rombului este 24a și latura rombului este 25a.

Apoi avem aria rombului: 25a.24a = 9 600 a2 = 16 a = 4 cm.

Înălțimea rombului este: 24,4 = 96 (cm).

Deci înălțimea rombului este de 96 cm.

Lecția 4: 

Având în vedere rombul ABCD cu lungimea laturii 12,5 cm, înălțimea 6,72 cm și AC este mai mic decât BD. Care sunt lungimile diagonalelor AC și respectiv BD?

Premiu:

Aplicați formula pentru a calcula aria unui romb: S = ha = 6,72 x 12,5 = 84 cm.
=> 1/2 AC x BD = 84 => 2AC.BD = 336

Fie O intersecția celor două diagonale ale unui romb.

Avem AOB este un triunghi dreptunghic la O ​​deci AB2 = OA2 + OB2

În care, OA = 1/2 AC, OB = 1/2 BD

=> 12,52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2+ 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (După problema BD > AC) (2)

Din (1) și (2), avem:

BD = 24, AC = 7cm.

Lecția 5: 

Rombul ABCD are laturile egale cu 10 unități. Calculați lungimea diagonalei rombului.

Rezolvare: Lungimea diagonalei rombului ABCD este:

Diagonală = rădăcină pătrată a lui 2(10²) = rădăcină pătrată a lui 200 = 14,14 unități de lungime.

Deci lungimea diagonalei rombului ABCD este de 14,14 unități de lungime.

Lecția 6:

Rombul ABCD are o diagonală de 12 unități. Calculați perimetrul rombului.

Soluție: Deoarece un romb are patru laturi egale, perimetrul său va fi suma lungimilor celor patru laturi, adică:

Perimetrul = 4 x lungime latura = 4 x 6 = 24 unități de lungime.

Deci perimetrul rombului ABCD este de 24 de unități de lungime.