Formula de calcul a ariei și perimetrului unui paralelogram este cunoștințele de bază. Vă rugăm să consultați formula pe care Quantrimang.com a compilat-o mai jos.
Cuprins
1. Aria paralelogramului
Aria unui paralelogram este măsurată prin dimensiunea suprafeței, care este partea plană vizibilă a paralelogramului.
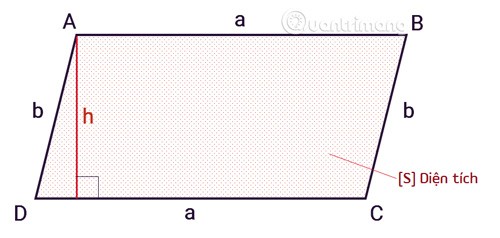
Aria unui paralelogram se calculează prin formula egală cu produsul bazei cu înălțimea.
SABCD = axh
Acolo:
Seste aria unui paralelogram.aeste baza paralelogramului.heste înălțimea, de la vârf la bază, a unui paralelogram.
2. Perimetrul paralelogramului
Perimetrul unui paralelogram se calculează prin adăugarea lungimii liniilor care înconjoară forma, care este și linia care înconjoară întreaga zonă, egală cu de 2 ori suma oricărei perechi de laturi adiacente.
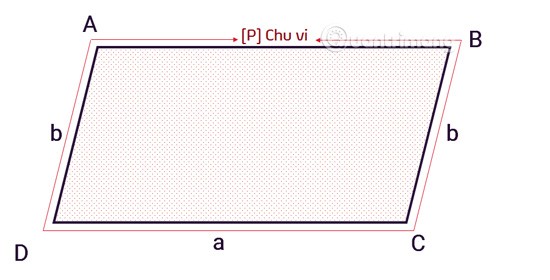
Cu alte cuvinte, perimetrul unui paralelogram este suma lungimilor celor patru laturi. Formula specifică este următoarea:
C = 2 x (a+b)
Acolo:
Ceste perimetrul unui paralelogram.ași bsunt laturile adiacente ale unui paralelogram.
3. Ce este un paralelogram?
Defini
Un paralelogram este un patrulater cu 2 perechi de laturi paralele sau 1 pereche de laturi paralele și egale. Un paralelogram are două unghiuri opuse egale și două diagonale care se intersectează la mijlocul formei.
Paralelogramul poate fi considerat un caz special de trapez.
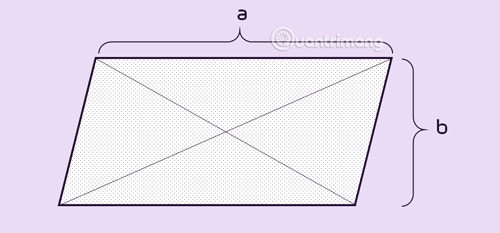
Proprietățile paralelogramului
În paralelogram:
- Laturile opuse sunt egale.
- Unghiurile opuse sunt egale.
- Două diagonale se intersectează la mijlocul fiecărei linii.
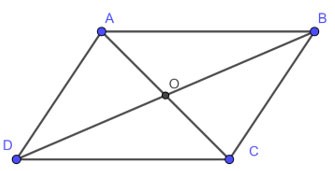
ABCD este un paralelogram, AC intersectează BD la O. Atunci:
• AB = CD, AD = BC
•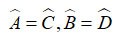
• OA = OC, OB = OD
Semne de recunoaștere
a) Un patrulater cu laturile opuse paralele este un paralelogram.
b) Un patrulater cu laturile opuse egale este un paralelogram.
c) Un patrulater cu două laturi opuse paralele și egale este un paralelogram.
d) Un patrulater cu unghiuri opuse egale între ele este un paralelogram.
e) Un patrulater cu două diagonale care se intersectează la mijlocul fiecăreia este un paralelogram.
4. Întrebări cu răspunsuri multiple pentru a revizui paralelogramele
Exercițiul 1 : Alegeți propoziția greșită.
A. Un paralelogram are două diagonale care se intersectează la mijlocul fiecărei diagonale.
B. Paralelogramul are două unghiuri opuse egale
C. Un paralelogram are două diagonale perpendiculare una pe cealaltă.
D. Două paralelograme au două perechi de laturi opuse paralele.
Soluţie
În paralelogram:
+ Paralelogramul are laturile opuse paralele
+ Laturile opuse sunt egale
+ Două diagonale se intersectează la mijlocul fiecărei linii, astfel încât C este incorect.
Răspunsul corect este: C
Exercițiul 2 : Dat paralelogramul ABCD cu  = α > 900. În afara paralelogramului, desenați triunghiuri echilaterale ADE, ABF. Ce fel de triunghi este triunghiul CEF? Alegeți cel mai bun răspuns
A. Triunghi
B. Triunghi isoscel
C. Triunghi echilateral
D. Triunghi obtuz
Răspuns:
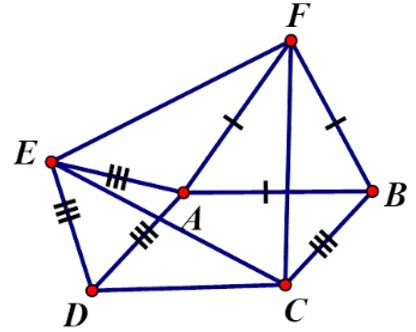

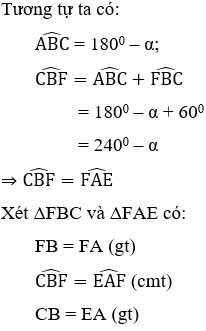
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
Din (1) și (2) putem deduce că CF = FE = EC, deci triunghiul CEF este echilateral.
Lecția 3 : Alegeți propoziția greșită. ABCD este un paralelogram. Apoi:
A. AB = CD
B. AD = BC
C. Test de paralelogram cu răspunsuri
D. AC = BD
Soluţie
În paralelogram:
+ Paralelogramul are laturile opuse paralele
+ Laturile opuse sunt egale
+ Două diagonale se intersectează la mijlocul fiecărei linii, astfel încât D este incorect.
Lecția 4 : Completați spațiul liber cu expresia potrivită: „Un patrulater cu două diagonale... este un paralelogram”.
A. egal
B. se intersectează
C. se intersectează la mijlocul fiecărei drepte
D. paralel
Soluţie
Semne:
Un patrulater cu două diagonale care se intersectează la mijlocul fiecăreia este un paralelogram.
Lecția 5 : Alegeți propoziția greșită:
A. Un patrulater cu două perechi de laturi opuse paralele este un paralelogram.
B. Un trapez cu două unghiuri egale adiacente unei baze este un paralelogram.
C. Un patrulater cu două perechi de laturi opuse egale este un paralelogram.
D. Un patrulater cu două perechi de unghiuri opuse egale este un paralelogram.
Soluţie
Semne:
+ Un patrulater cu laturile paralele opuse este un paralelogram, deci A este corect.
+ Un patrulater cu laturile opuse egale este un paralelogram, deci D este corect.
+ Un patrulater cu unghiuri opuse egale între ele este un paralelogram, deci D este corect.
Realizând că un trapez cu două unghiuri egale adiacente unei baze este un trapez isoscel, deci B este incorect.
Raspunsul corect este: B
5. Exemple de calculare a perimetrului și a ariei paralelogramului
Exemplul 1 : dat un paralelogram cu o bază de 12 cm, o latură de 7 cm și o înălțime de 5 cm. Calculați perimetrul și aria acelui paralelogram?
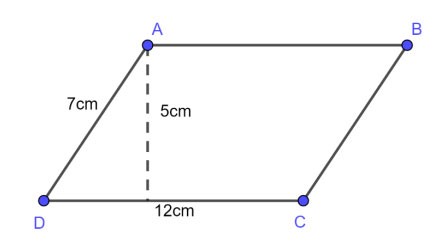
Premiu:
Perimetrul paralelogramului este:
P = 2 x (12 + 7) = 38 (cm)
Aria unui paralelogram este:
S = axh = 12 x 5 = 60 (cm2)
Exemplul 2:
Dat paralelogramul ABCD cu H, K fiind picioarele altitudinilor trase de la vârfurile A, C la BD, respectiv.
a) Demonstrați că AHCK este un paralelogram.
b) Fie O punctul de mijloc al lui HK. Demonstrați că A, O, C sunt coliniare.
Instrui:
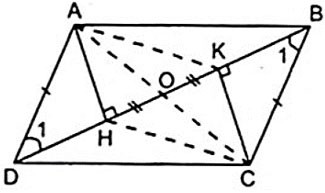
a) Din ipoteză avem:
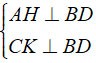 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 )
Aplicând proprietățile laturilor paralelogramelor și proprietățile unghiurilor alternative, avem:
 ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK
(hipotenuza – caz cu unghi acut)
⇒ AH = CK (laturile corespunzătoare sunt egale) ( 2 )
Din (1) și (2) avem patrulaterul AHCK cu laturile opuse paralele și egale este un paralelogram.
b) Aplicați proprietățile diagonalelor paralelogramului AHCK
Paralelogramul AHCK are două diagonale AC și HK care se intersectează la mijlocul fiecărei linii. Deoarece O este punctul de mijloc al lui HK, O este și punctul de mijloc al lui AC.
⇒ A, O, C sunt pe o linie dreaptă.
Pe lângă paralelograme, formulele pentru calcularea ariei și a perimetrului altor forme geometrice comune, cum ar fi romburi , pătrate , trapeze , dreptunghiuri ... sunt, de asemenea, foarte importante și aplicate pe scară largă în studiu și viață.
Sperăm că, prin articolul de mai sus, ați înțeles și ați înțeles mai bine cunoștințele de bază despre paralelograme. Vă rugăm să lăsați un comentariu mai jos dacă aveți întrebări sau comentarii de discutat cu Quantrimang.com.



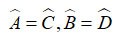



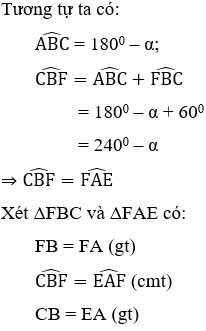


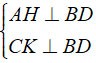 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 ) ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK