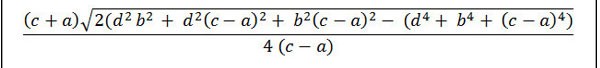Un trapez este un patrulater convex cu două laturi paralele, numite baze, iar laturile rămase se numesc laturile laterale. Formula de calcul a perimetrului și a ariei unui trapez este una dintre cunoștințele matematice de bază care se aplică frecvent atât în studiu, cât și în viață. Următorul articol vă va prezenta formula pentru calcularea ariei unui trapez și a lungimii bazei unui trapez, vă rugăm să consultați aceasta.
Cuprins
Există un trapez ABCD cu lungimea de bază AB a, lungimea de bază CD b și înălțimea h.
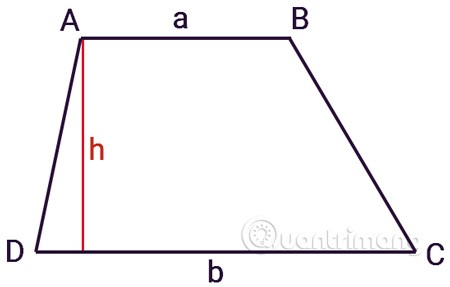
Aria unui trapez este egală cu media celor două baze înmulțită cu înălțimea dintre cele două baze.
Acolo:
Există, de asemenea, o poezie despre calcularea ariei unui trapez, care este destul de ușor de reținut, după cum urmează:
Vrei să calculezi aria unui trapez
Adăugăm fundul mare și fundul mic împreună.
Adunați și înmulțiți cu înălțimea
Împărțiți în jumătate și luați în jumătate, oricum va ieși.
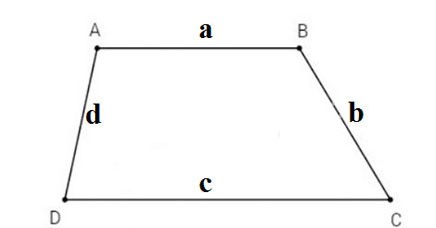
În cazul în care problema oferă date despre lungimea a 4 laturi, indicând clar latura de bază a, c cu latura de bază c fiind mai mare decât latura de bază a, laturile laterale sunt b și d, atunci puteți calcula aria trapezului folosind următoarea formulă.
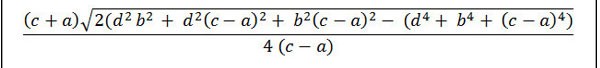
Acolo:
Un trapez drept este un trapez care are un unghi drept. Latura perpendiculară pe cele două baze este și înălțimea h a trapezului.
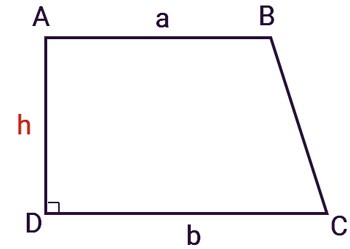
Formula generală pentru calcularea ariei unui trapez drept este similară cu cea a unui trapez obișnuit: media celor două laturi ale bazei înmulțită cu înălțimea dintre cele două baze , totuși înălțimea aici este latura perpendiculară pe ambele baze.
Acolo:
Un trapez isoscel este un trapez ale cărui două unghiuri adiacente sunt egale. Cele două laturi ale unui trapez sunt egale și nu sunt paralele între ele.
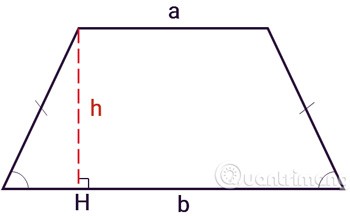
Pe lângă aplicarea formulei ca de obicei pentru a calcula un trapez, puteți, de asemenea, să împărțiți trapezul isoscel în părți mai mici pentru a calcula aria fiecărei părți și apoi să le adăugați.
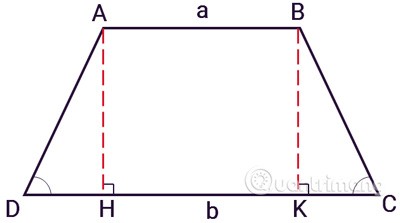
De exemplu, trapezul isoscel ABCD are două laturi egale AD și BC. Cu înălțimile AH și BK, trapezul va fi împărțit în 1 dreptunghi ABKH și 2 triunghiuri ADH și BCK. Aplicați formula pentru calcularea aria unui dreptunghi pentru ABHK și aria unui triunghi pentru ADH și BCK, apoi adăugați toate ariile pentru a găsi aria trapezului ABCD.
Mai exact așa:
Și SADH = SBCK (ușor de demonstrat), obținem:
Cunoscând aria, înălțimea și lungimea unei laturi a bazei, puteți calcula lungimea laturii rămase după cum urmează:
Exemplul 1: Calculați aria unui trapez
Calculați aria unui trapez știind că lungimile celor două baze sunt de 18cm și respectiv 14cm; inaltimea este de 9 cm
Premiu:
Aplicând formula pentru calcularea ariei unui trapez avem:
Deci aria trapezului este de 144 cm2
Exemplul 2:
Există o bucată de teren trapezoidală cu o bază mică de 24 m și o bază mare de 30 m. Extindeți cele două baze din dreapta terenului cu baza mai mare adăugată 7m, baza mai mică adăugată 5m pentru a obține un nou teren trapezoidal cu o suprafață cu 36m2 mai mare decât suprafața inițială. Calculați aria terenului trapezoid inițial.
Premiu:
Conform problemei, aria crescută este aria unui trapez cu o bază mare de 7 m și o bază mică de 5 m. Prin urmare, înălțimea terenului trapezoidal este: h = (36 x 2) : (7 + 5) = 6m
Suprafața de teren inițială este: S = 6 . (24 + 30) : 2 = 162 m²
Lecția 3:
Având în vedere un trapez drept cu o distanță între cele două baze de 16 cm, baza mică este ¾ din baza mare. Calculați lungimea celor 2 baze știind că aria trapezului drept este de 112 cm².
Premiu:
Distanța dintre cele două baze dintr-un trapez drept este înălțimea trapezului, deci:
Lungimea totală a celor două baze este (112 x 2): 16 = 14cm
Numim lungimea bazei mici a, lungimea bazei mari b, avem:
a + b = 14 și a = ¾ b
Deci a = 14 x 4: 7 = 8cm
Asadar, baza mica = 34/7 cm, baza mare 64/7 cm
Exemplul 4: Trapezul isoscel ABCD (AB//CD) are AB = 5cm, CD = 13cm, AD = 5cm. Calculați aria trapezului ABCD?
Premiu:
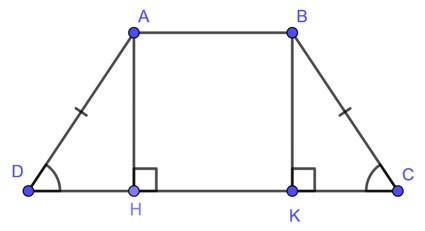
Fie AH și BK cele două înălțimi ale trapezului. Atunci, ABKH este un dreptunghi pe care avem:
Aplicând teorema lui Pitagora triunghiului dreptunghic AHD avem:
Deci: AH = 3cm
Deci aria trapezului ABCD este:
Mai sus este un articol de Quantrimang.com despre cea mai standard formulă și modalitatea de a calcula aria unui trapez. Sper că acest articol vă este util!
Compară activități secundare realiste pentru 2026 în funcție de costul de pornire, comisioane, flexibilitate și controlul veniturilor, cu îndrumări actuale privind impozitele și escrocheriile din surse oficiale.
Îmbunătățiți-vă ergonomia biroului de acasă cu îndrumările OSHA și NIOSH actuale privind potrivirea scaunului, înălțimea monitorului, configurarea laptopului, iluminarea și mișcarea.
Află de ce contează inteligența emoțională în leadership, unde ajută cel mai mult, cum să o consolidezi și cum să-ți dai seama dacă abordarea ta funcționează.
O foaie de parcurs practică pentru a intra în domeniul tehnologiei fără diplomă: alege un rol accesibil, dezvoltă abilități pregătite pentru angajare, demonstrează-le prin proiecte și folosește feedback-ul de la angajare pentru a te îmbunătăți.
Build a credible LinkedIn personal brand in 2026 with current profile, content, newsletter, analytics, verification, and visibility guidance from LinkedIn.
Demisiile discrete și concedierile discrete sunt etichete atrăgătoare, nu diagnostice. Aflați ce se verifică, ce depinde de context și ce pot face angajații și managerii în continuare.
Directorii executivi fracționari oferă funcții de conducere fără angajare cu normă întreagă. Învață când funcționează modelul, ce să ceri și riscurile de gestionat.
Pregătiți o cerere de mărire salarială mai convingătoare pentru trimestrul 4, incluzând date salariale actuale, opțiuni de sincronizare, compromisuri salariale și scenarii pentru rezultate afirmative, parțiale sau negative.
Choose a high-income skill you can realistically start before 2026 ends, with current pay data, learning priorities, and a practical self-check.
Construiește un program de lucru hibrid în jurul sarcinilor, suprapunerii echipei și rezultatelor măsurabile. Vezi modele, semne de avertizare și când să-ți ajustezi planul.
