Formula pentru calcularea înălțimii în triunghiuri regulate, isoscel, echilaterale și dreptunghiulare

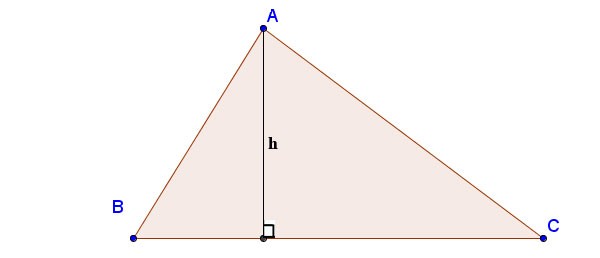
Altitudinea într-un triunghi este o linie dreaptă cu proprietăți importante și este strâns legată de problemele de geometrie plană. Deci, care este înălțimea, cum se calculează înălțimea într-un triunghi? Vă rugăm să consultați articolul de mai jos pentru răspuns și cea mai simplă formulă pentru calcularea înălțimii unui triunghi.

Cuprins

• Formula pentru calcularea înălțimii într-un triunghi
  • Calculați înălțimea într-un triunghi regulat
  • Calculați înălțimea într-un triunghi echilateral
  • Formula pentru calcularea înălțimii într-un triunghi dreptunghic
  • Formula pentru calcularea înălțimii într-un triunghi isoscel
• Definiția altitudinii într-un triunghi
• Proprietățile celor trei altitudini ale unui triunghi

Formula pentru calcularea înălțimii într-un triunghi

Calculați înălțimea într-un triunghi regulat

Cum se calculează înălțimea unui triunghi folosind formula lui Heron:

Cu a, b, c fiind lungimile laturilor; ha este altitudinea trasată de la vârful A la latura BC; p este semiperimetrul:

De exemplu: 

Triunghiul dat ABC, latura AB = 4 cm, latura BC = 7 cm, latura AC = 5 cm. Calculați altitudinea AH de la A intersectând BC la H și calculați aria lui ABC.

Premiu:

Jumătate de perimetru al triunghiului: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Înălţime   

=>

Luați în considerare triunghiul ABC, avem:

Aşa,

Calculați înălțimea într-un triunghi echilateral

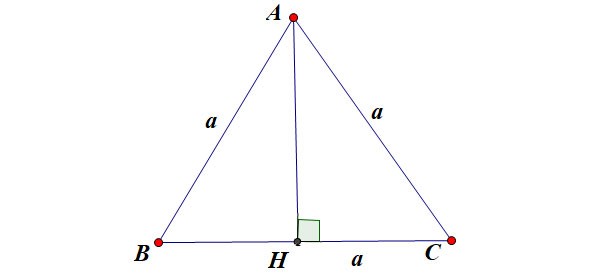
Să presupunem că triunghiul echilateral ABC are lungimea laturii a așa cum se arată în figură:

Acolo:

• h este înălțimea unui triunghi echilateral
• a este lungimea laturii unui triunghi echilateral

Formula pentru calcularea înălțimii într-un triunghi dreptunghic

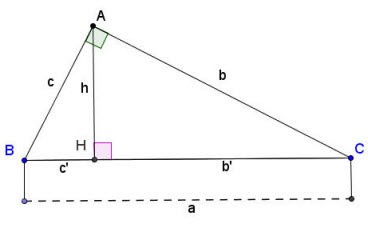
Să presupunem că există un triunghi dreptunghic ABC drept la A, așa cum se arată mai sus:

Formula pentru calcularea laturilor și înălțimii într-un triunghi dreptunghic:

1. a2 = b2 + c2

2. b2 = ab′ și c2 = ac′

3. ah = bc

4. h2 = b′.c'

5.

Acolo:

• a, b, c sunt laturile unui triunghi dreptunghic așa cum se arată mai sus;
• b' este proiecția muchiei b pe ipotenuză;
• c' este proiecția muchiei c pe ipotenuză;
• h este înălțimea unui triunghi dreptunghic trasat de la vârful unghiului drept A până la ipotenuza BC.

Exemplul 1: Triunghiul dat ABC dreptunghic la A, înălțimea AH. Calculați BC, AC, AH știind AB = 15cm, HC = 16cm.

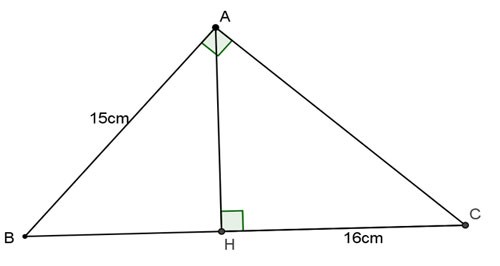
Premiu:

Aplicând formula algebrică în triunghiul dreptunghic ABC avem:

AC2 = CH.BC = 16.BC

Conform teoremei lui Pitagora pentru triunghiul dreptunghic ABC cu unghi drept A avem:

AB2 + AC2 = BC2

⇔ 152 + 16.BC = BC2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 sau BC = -9 (elimină)

⇒ AC2 = 16.BC = 16,25 = 400 ⇒ AC = 20 (cm)

Considerăm triunghiul dreptunghic ABC cu: AH.BC = AB.AC (formula geometrică)

=> AH = AB.AC/BC = 15,20/25 = 12(cm)

Deci BC=25(cm); AC=20(cm); AH=12(cm)

Exemplul 2 :

Triunghiul dat ABC este dreptunghic la A, AB=24cm, AC=32cm. Bisectoarea perpendiculară a lui BC intersectează AC, BC la D și, respectiv, E. Calculați DE.

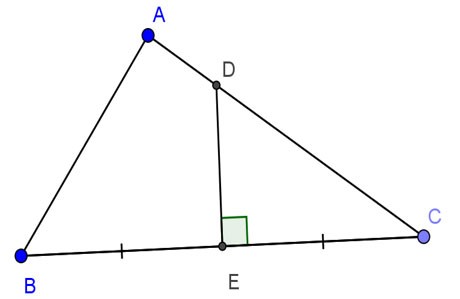
Premiu:

Luați în considerare triunghiul dreptunghic ABC, avem:

BC2 = AB2 + AC2 (conform teoremei lui Pitagora)

BC2 = 242+ 322

BC2 = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20 (cm)

Luați în considerare triunghiul dreptunghic ACB și triunghiul dreptunghic ECD cu:

Există ∠A = ∠E = 90o

∠C comun

=> Triunghi ACB ∾ triunghi ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Deci ED = 15cm

Formula pentru calcularea înălțimii într-un triunghi isoscel

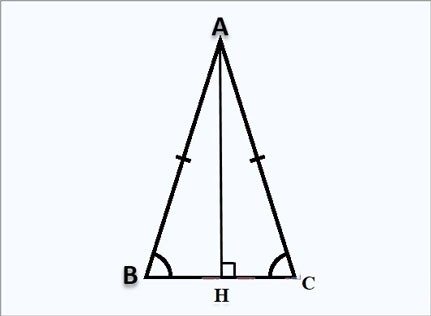
Să presupunem că aveți un triunghi isoscel ABC la A, înălțimea AH este perpendiculară la H așa cum se arată mai sus:

Formula pentru calcularea înălțimii AH:

Deoarece triunghiul ABC este isoscel la A, înălțimea AH este și mediana, deci:

⇒ HB=HC= ½BC

Aplicând teorema lui Pitagora în triunghiul dreptunghic ABH drept la H avem:

AH²+BH²=AB²

⇒AH²=AB²−BH²

De exemplu : dat Δ ABC este echilibrat la A cu BC = 30(cm), înălțimea AH = 20(cm). Calculați înălțimea corespunzătoare laturii acelui triunghi isoscel.

Rezolvare: Considerăm Δ ABC este isoscel la A cu BC = 30(cm)

⇒ BH = CH = 15(cm).

Aplicând teorema lui Pitagora avem:

Acum trebuie să calculăm BK = ?

Avem:

Pe de altă parte

Prin urmare, avem ⇔

Definiția altitudinii într-un triunghi

O altitudine într-un triunghi este un segment perpendicular trasat de la un vârf pe latura opusă. Această latură opusă se numește baza corespunzătoare altitudinii. Lungimea altitudinii este distanța dintre partea de sus și de jos.

Proprietățile celor trei altitudini ale unui triunghi

Cele trei altitudini ale unui triunghi trec prin același punct. Acest punct se numește ortocentrul triunghiului .

Trebuie doar să calculați componentele necunoscute din formulele de mai sus pentru a calcula înălțimea unui triunghi pentru a putea calcula înălțimea unui triunghi.

• Care este focalizarea? Formula pentru calcularea centrului de centru al unui triunghi