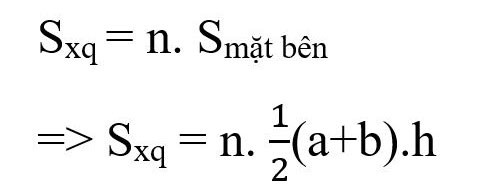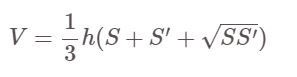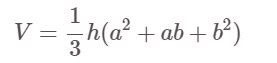Să învățăm ce este o piramidă trunchiată, cum să calculăm volumul unei piramide trunchiate, aria laterală și aria totală a unei piramide trunchiate în articolul de mai jos.
Cuprins
Definiţia frustum
O trunchi de piramidă este o parte a unui poliedru, situată între bază și secțiunea transversală tăiată de un plan paralel cu baza piramidei.
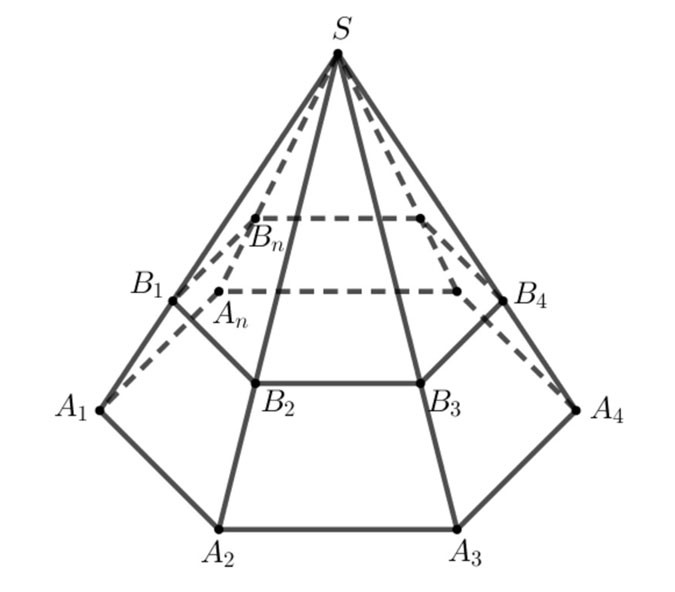
- Figura formată din poligoane A1A2...An,B1B2...BnA1A2...An,B1B2...Bn și trapeze A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B3B3B2,...,AnA1B2Bn este denumită ca truncă amidă. A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
- Mai simplu spus, din piramida S.A1A2...AnS.A1A2...An după tăierea piramidei S.B1B2...Bn.S.B1B2...Bn se formează o piramidă trunchiată.
+ Poligoanele A1A2...An,B1B2...BnA1A2...An,B1B2...Bn se numesc cele două baze,
+ Trapezele A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn se numesc fețe laterale.
+ Segmentele de linie A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn se numesc margini laterale, marginile suprafetei de baza se numesc margini de baza.
+ Distanța dintre cele două baze se numește înălțimea piramidei trunchiate.
Proprietățile piramidei trunchiate:
- Cele două baze sunt două poligoane (triunghiuri, patrulatere, pentagoane etc.) cu laturile paralele corespunzătoare și rapoarte egale ale laturilor corespunzătoare.
- Fețele laterale sunt toate trapeze.
- Liniile care conțin marginile laterale vor converge într-un punct (partea de sus a piramidei).
- O piramidă trunchiată este o piramidă ale cărei baze sunt poligoane regulate (cu laturi egale). Prin urmare, fețele laterale ale unui tronc sunt toate trapeze egale.
Formula pentru calcularea ariei unei piramide trunchiate
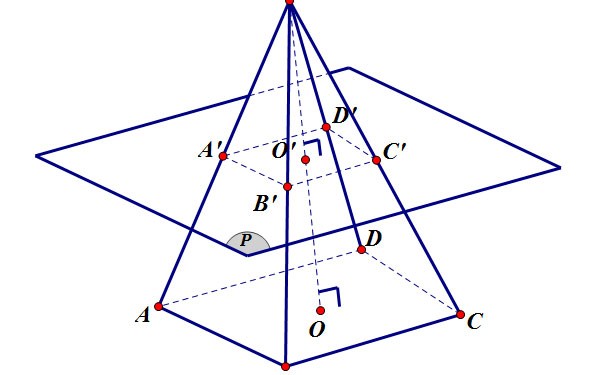
Suprafața piramidei trunchiate
Aria laterală a unei piramide trunchiate este aria fețelor înconjurătoare, partea care înconjoară piramida trunchiată, excluzând zona celor două baze.
Cum se calculează aria laterală a unei piramide trunchiate: Calculați aria fiecărei fețe laterale (trapeze) a piramidei trunchiate conform formulei de calcul a ariei unui trapez normal , apoi calculați aria totală.
Formula pentru calcularea ariei unei piramide trunchiate obișnuite:
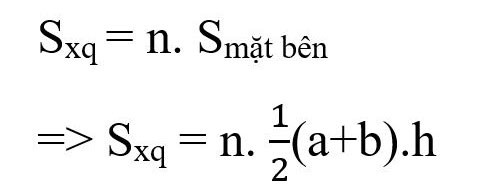
Acolo:
- Sxq: zona înconjurătoare
- n: numărul de fețe laterale ale piramidei trunchiate (egal cu numărul de muchii ale poligonului de bază)
- a, b: lungimile laterale ale bazei superioare și respectiv inferioare
- h: înălțimea patrulaterelor laterale.
Exemplul 1:
Calculați aria laterală a unei piramide trunchiate patrulatere regulate cu marginile bazei de 10 cm și 15 cm și înălțimea laterală de 12 cm.

Premiu:
Fața laterală a unei piramide trunchiate patrulatere obișnuite este un trapez isoscel, deci aria unei fețe laterale este:
O piramidă trunchiată patrulateră obișnuită are 4 laturi egale, deci aria sa laterală este:
150 x 4 = 600 (cm2)
Exemplul 2: Calculați aria laterală a unei piramide trunchiate patrulatere regulate cu marginile bazei de 6cm și 8cm și înălțimea laterală de 5cm. Calculați aria laterală a unei piramide trunchiate patrulatere regulate cu marginile bazei de 6cm și 8cm.

Premiu:
Fața laterală a unei piramide trunchiate patrulatere obișnuite este un trapez isoscel, deci aria unei fețe laterale este egală cu
O piramidă trunchiată patrulateră obișnuită are patru laturi egale, astfel încât aria sa laterală este egală cu
35 x 4 = 140 (cm2)
Suprafața totală a unei piramide trunchiate
Aria totală a unei piramide trunchiate este egală cu suma ariei laterale și aria celor două baze.
Formula: Stp = Sxq + fund mare + fund mic
Acolo:
- Stp: Suprafața totală
- Sxq: Zona înconjurătoare
- Baza mare: zonă mare de bază
- Baza mică: zonă mică de bază
De exemplu:
Calculați aria totală a unei piramide trunchiate obișnuite conform dimensiunilor date în figură.
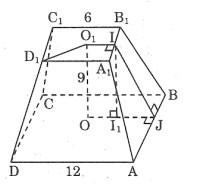
Premiu:
Avem:
AD = 12 ⇒ OJ = 6
Desenarea II1 ⊥ OJ avem: I1J = 3
Aplicând teorema lui Pitagora triunghiului dreptunghic II1J avem:
IJ2 = II12 + I1J2 = 92 + 32 = 90
Prin urmare:
Aria unei laturi a unui trapez este:
Zona înconjurătoare este egală cu:
Aria bazei superioare este: S = 6 x 6 = 36 (unități)
Aria bazei inferioare este: S = 12 x 12 = 144 (unități)
Aria totală a unei piramide trunchiate este egală cu:
Formula pentru calcularea volumului unei piramide trunchiate
Reţetă:
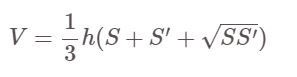
Acolo:
- V: volumul piramidei trunchiate
- S, S' sunt zonele bazelor mari și, respectiv, mici ale piramidei.
- h: înălțimea piramidei, adică distanța dintre cele două baze mari și mici
O piramidă trunchiată este un pătrat (padrulateral regulat):
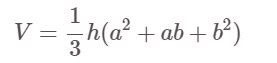
Acolo:
- V: Volumul
- h: Înălțimea piramidei
- a, b sunt lungimile marginilor bazei mari și, respectiv, ale bazei mici.