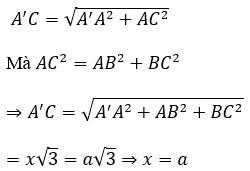O prismă este un poligon cu două baze paralele și egale și fețe laterale paralelograme.
Comentariu:
- Fețele laterale ale unei prisme sunt egale și paralele între ele.
- Fețele laterale sunt paralelograme.
- Cele două baze ale unei prisme sunt două poligoane egale.
Care este formula de calcul a volumului unei prisme (prismă V) și care este formula de calcul a volumului unei prisme verticale? Vă rugăm să consultați articolul de mai jos.
Cuprins
1. Volumul unei prisme verticale
Formula pentru calcularea volumului unei prisme verticale:
Volumul unei prisme drepte este egal cu produsul ariei bazei înmulțit cu înălțimea.
Acolo
Veste volumul prismei (unitatea m3)Beste suprafața de bază (unitatea m2)heste înălțimea prismei (unitatea m)
3. Clasificarea prismelor
Prismă obișnuită
Este o prismă verticală cu o bază poligonală regulată. Fețele laterale ale prismei sunt toate dreptunghiuri egale. De exemplu: prisma triunghiulara regulata, patrulaterul regulat... atunci il intelegem ca fiind o prisma regulata.
O bază patrulateră regulată se numește prismă patrulateră regulată.
Prismă triunghiulară
- O prismă triunghiulară are 5 fețe, 9 muchii și 6 vârfuri.
- Cele două baze sunt ambele triunghiulare și paralele între ele; Fiecare față laterală este un dreptunghi;
- Laturile sunt egale;
- Înălțimea unei prisme triunghiulare este lungimea unei laturi.
De exemplu:
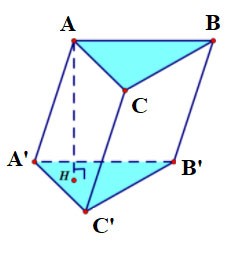
Prisma triunghiulară ABC.A'B'C' are:
- Baza de jos este triunghiul ABC, baza de sus este triunghiul A'B'C';
Fețele laterale sunt dreptunghiuri: AA'B'B, BB'C'C, CC'A'A;
- Margini:
- Margini de bază: AB, BC, CA, A'B', B'C', C'A'
- Laturi: AA', BB', CC';
- Nodurile: A, B, C, A', B', C'.
- Înălțimea este lungimea unei laturi: AA' sau BB' sau CC'.
Prisma patrulateră
- O prismă patrulateră are 6 fețe, 12 muchii și 8 vârfuri.
- Cele două baze sunt ambele patrulatere și paralele între ele. Fiecare față laterală este un dreptunghi.
- Laturile sunt egale.
- Înălțimea unei prisme patrulatere este lungimea unei laturi.
De exemplu:
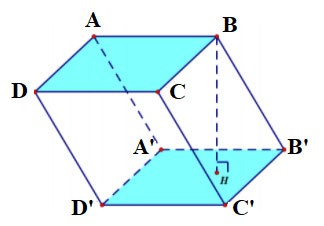
Prisma patrulateră ABCD.A'B'C'D' are:
- Baza de jos este patrulater ABCD, baza de sus este patrulater A'B'C'D';
Fețele laterale sunt dreptunghiuri: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Margini:
+ Margini de bază: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Marginile laterale: AA', BB', CC', DD' sunt egale.
- Nodurile: A, B, C, D, A', B', C', D'.
- Înălțimea este lungimea unei laturi: AA' sau BB' sau CC' sau DD'.
Notă: prismele și cuburile dreptunghiulare sunt, de asemenea, prisme patrulatere.
Prisma dreapta
Dacă o prismă are margini laterale perpendiculare pe bază, se numește prismă dreaptă.
Nota:
Dacă baza este un dreptunghi, cilindrul vertical al patrulaterului se numește cutie dreptunghiulară.
Dacă un cilindru patrulater are 12 laturi de lungime a, atunci numele său este un cub.
Comparați prisma dreaptă și prisma regulată:
| DEFINI: |
NATURĂ |
| + O prismă verticală este o prismă cu latura perpendiculară pe bază. |
+ Fețele laterale ale unei prisme verticale sunt dreptunghiulare.
+ Fețele laterale ale prismei sunt perpendiculare pe fața de bază.
+ Înălțimea este partea laterală
|
| + O prismă regulată este o prismă verticală a cărei bază este un poligon regulat. |
+ Fețele laterale ale unei prisme sunt toate dreptunghiuri egale.
+ Înălțimea este partea laterală
|
4. Exemplu de calcul al volumului unei prisme verticale
Exemplul 1:
Prisma dată ABC.A'B'C' cu baza ABC fiind un triunghi echilateral cu latura a = 2 cm și înălțimea h = 3 cm. Calculați volumul acestei prisme?
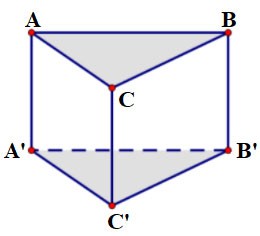
Premiu:
Deoarece baza este un triunghi echilateral cu latura a, aria este:
În acest moment, volumul prismei este:
Exemplul 2:
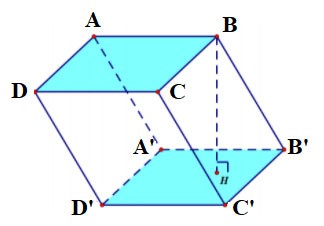
Exercițiul 1: Având în vedere o cutie verticală cu muchiile AB = 3a, AD = 2a, AA'= 2a. Calculați volumul blocului A'.ACD'
Instrui:
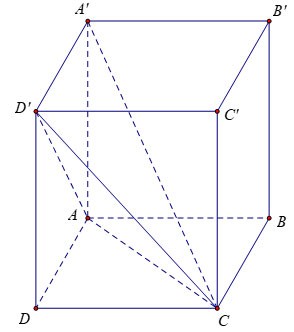
Deoarece fața laterală ADD'A' este un dreptunghi, avem:
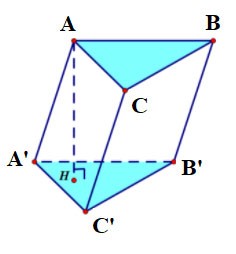
Exemplul 3 : Având în vedere o prismă verticală ABC.A'B'C' a cărei bază este un triunghi echilateral cu latura a√3, unghiul dintre bază și prismă este de 60º. Fie M punctul de mijloc al lui BB'. Calculați volumul piramidei M.A'B'C'.
Premiu:
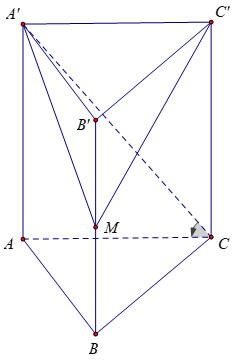
Prin urmare, putem deduce că
Avem:
Exemplul 4:
Având în vedere o prismă patrulateră regulată ABCD.A'B'C'D' cu marginea bazei de lungimea a și fața (DBC') care formează un unghi de 60º cu baza ABCD. Calculați volumul prismei ABCD.A'B'C'D?
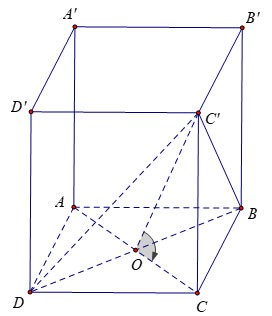
Avem: în centrul O al pătratului ABCD.
Pe de altă parte deci
Deduce
Asemenea:
Exemplul 5:
Calculați volumul V al cubului ABCD.A'B'C'D', cunoscând AC'=a√3
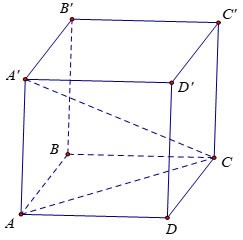
Premiu:
Fie x lungimea laturii cubului.
Considerăm triunghiul AA'C dreptunghic la A cu:
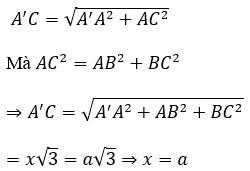
Prin urmare, volumul cubului este V=a^3.
În plus față de formula de calcul a volumului unei prisme de mai sus, puteți consulta mai multe articole despre formula de calculare a volumului unui solid de revoluție , formula de calcul a ariei și circumferinței unui cerc ...