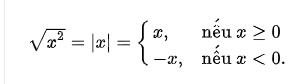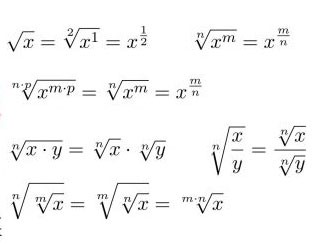Rădăcina pătrată este una dintre cunoștințele importante în matematică utilizate pe parcursul procesului de învățare al elevilor. Următorul articol vă va prezenta definiția a ceea ce este o rădăcină pătrată și cum se calculează rădăcina pătrată a unui număr? Vă rugăm să consultați.
Cuprins
Ce este rădăcina pătrată?
Rădăcina pătrată a unui număr a este un număr x astfel încât x2 = a, sau cu alte cuvinte, numărul x a cărui valoare pătrată = a.
De exemplu, 2 și −2 sunt rădăcini pătrate ale lui 2 deoarece 2² = (−2)² = 4.
Semnul radical este notat cu √.
- Fiecare număr real nenegativ a are o rădăcină pătrată nenegativă unică, numită rădăcină pătratică aritmetică.
De exemplu, rădăcina pătrată aritmetică a lui 16 este 4, notată cu √16 = 4, deoarece 4² = 4 × 4 = 16 și 4 este un număr nenegativ.
Fiecare număr pozitiv a are două rădăcini pătrate: √a este o rădăcină pătrată pozitivă și −√a este o rădăcină pătrată negativă. Ele sunt notate simultan ca ± √a.
Cele mai simple calcule de rădăcină pătrată
Amintiți-vă câteva numere pătrate de bază și cele mai comune, astfel încât, atunci când luați rădăcini pătrate, puteți calcula mai repede în cap:
0² = 0
1² = 1
3² = 9
4² = 16
5² = 25 6² = 36
7² = 49
8² = 64
9² =
81 10² =
100
11² = 121 12²
= 144
13² = 16914 =
1691² = 1691²
= 16912²
16² = 256
17² = 289
Câteva formule de bază de rădăcină pătrată pe care toată lumea ar trebui să le amintească includ:
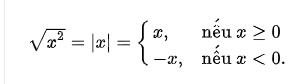
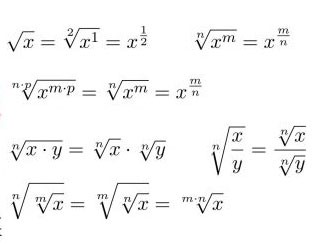
Tabel cu rădăcină pătrată
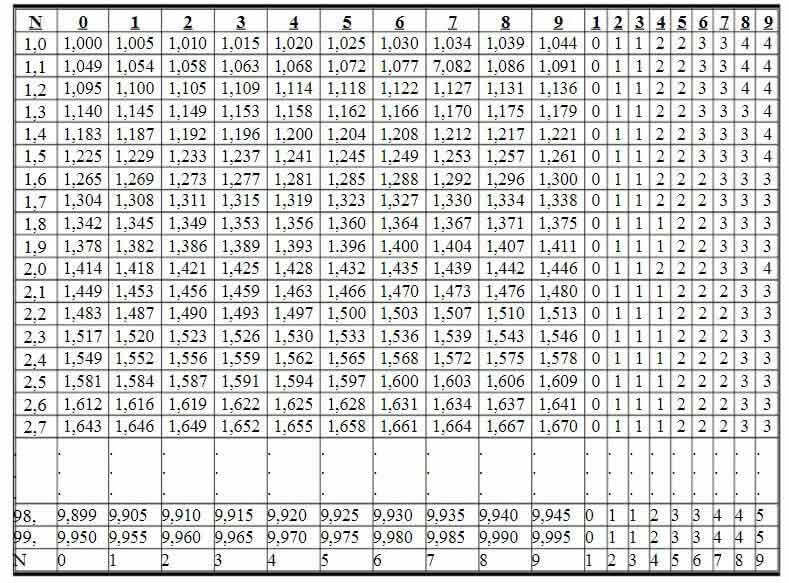
Tabelul cu rădăcină pătrată este împărțit în rânduri și coloane, permițând găsirea directă a rădăcinii pătrate a numerelor mai mari de 1 și mai mici de 100.
Rădăcinile pătrate ale numerelor scrise cu cel mult trei cifre de la 1,00 la 99,9 sunt date în tabel în coloanele de la 0 la 9. În continuare sunt nouă coloane de corecție utilizate pentru a corecta ultima cifră a rădăcinilor pătrate a numerelor scrise cu patru cifre de la 1.000 la 99.99.
Exemplul 1: Găsiți
→ Soluție:
La intersecția rândurilor 1,4 și coloanei 1 vedem numărul 1.187
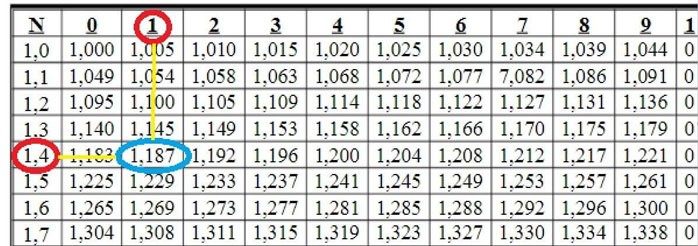
Aşa
Exemplul 2:
Găsi
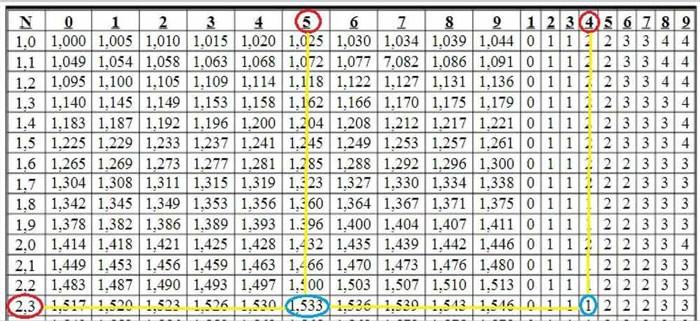
La intersecția rândurilor 2,3 și coloanei 5 vedem numărul 1.533. Avem
Apoi, la intersecția rândurilor 2,3 și coloana 4, vedem numărul 1. Acest număr 1 este folosit pentru a corecta ultima cifră din numărul . Adică: 1,533 + 0,001 = 1,534
Aşa
Cum se calculează rădăcina pătrată fără a folosi calculatorul
Găsiți rădăcina pătrată a unui număr întreg
Găsiți rădăcina pătrată prin înmulțire.
Rădăcina pătrată a unui număr este numărul care, atunci când înmulțiți numărul cu el însuși, vă oferă numărul inițial.
Deci asta înseamnă „Ce număr poți înmulți singur pentru a obține numărul pe care îl ai deja?”
De exemplu:
Rădăcina pătrată a lui 1 este 1 deoarece 1 ori 1 este egal cu 1 (1 X 1 = 1).
Rădăcina pătrată a lui 4 este 2 pentru că de 2 ori 2 este egal cu 4 (2 X 2 = 4).
Rădăcina pătrată a lui 9 este 3 deoarece 3 x 3 = 9.
Folosiți diviziunea pentru a găsi rădăcina pătrată
Pentru a găsi rădăcina pătrată a unui număr întreg, puteți împărți numărul întreg la numere succesive până când găsiți un coeficient care este exact același cu divizorul dvs.
De exemplu:
16 împărțit la 4 este 4, deci 4 este rădăcina pătrată a lui 16.
4 împărțit la 2 este 2, deci 2 este rădăcina pătrată a lui 4.
Găsiți rădăcina pătrată a altor numere
Ghiciți și apoi folosiți procesul de eliminare.
Exemplu: Găsiți rădăcina pătrată a lui 20.
Între timp, știm că 16 este un număr pătrat perfect cu rădăcina pătrată 4 (4X4=16).
25 are și rădăcina pătrată de 5 (5X5=25).
Deci am ghici că rădăcina pătrată a lui 20 ar fi undeva între 4 și 5.
Putem ghici că rădăcina pătrată a lui 20 este 4,5 și încercați să puneți la pătrat 4,5 pentru a verifica. Adică, luați 4,5 x 4,5, dacă răspunsul nu este 20, atunci vedem dacă rezultatul este mai mare sau mai mic de 20 pentru a calcula. Dacă este mai mic de 20, atunci continuăm să încercăm cu 4, 6 și numere mai mari. Dacă rezultatul este mai mare de 20, atunci încercați să calculați cu 4,4 și numere mai mici până când obțineți rezultatul corect.
Rezultatul acestui calcul este 4,475 X 4,475 = 20,03. Când rotunjiți în jos, răspunsul este 20.
Cum se compară rădăcinile pătrate
Cu oricare 2 numere pozitive a și b
Dacă a = b atunci
Dacă a > b atunci
Dacă un < b="" atunci="">
De exemplu:
Comparați și
Pentru că 21 < 31,
Sperăm că articolul de mai sus te-a ajutat să înțelegi cunoștințele despre rădăcinile pătrate, cum să calculezi, cum să compari... pentru a rezolva exerciții despre rădăcinile pătrate, precum și alte exerciții conexe.