Să învățăm despre formula de calcul a ariei laterale, a suprafeței totale și a înălțimii unui cilindru de aplicat în studiu și viața de zi cu zi.
Cuprins
Cum se calculează aria unui cilindru
Aria unui cilindru include aria laterală și aria totală.
Puteți introduce înălțimea și raza cilindrului în tabelul de mai jos pentru a cunoaște aria laterală și aria totală a cilindrului.
Formula pentru calcularea ariei laterale a unui cilindru
Zona laterală a unui cilindru include numai zona suprafeței înconjurătoare care înconjoară cilindrul, fără a include zona celor două baze.
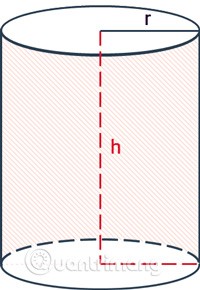
Formula pentru calcularea ariei laterale a unui cilindru este circumferința cercului de bază înmulțită cu înălțimea.
 |
Acolo:
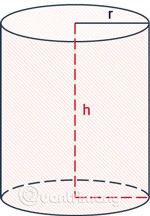
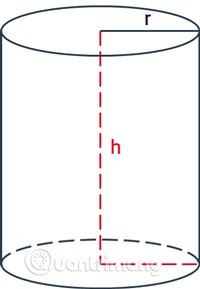
- În jur este zona înconjurătoare.
reste raza cilindrului.heste înălțimea, distanța dintre cele două baze ale cilindrului.
|
Exemplu: 1
Un cilindru circular are raza bazei r = 5 cm, înălțimea h = 7cm. Calculați aria laterală a unui cilindru vertical.
Rezolvare: Aria suprafeței unui cilindru circular: Sxq = 2.π.rh = 2π.5.7 = 70π = 219.8 (cm2).
Exemplu: 2
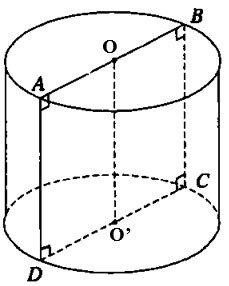
Dat pătratul ABCD cu latura 2a. Fie O și O’ punctele medii ale laturilor AB și, respectiv, CD. Când rotim acel pătrat în jurul axei OO', obținem un cilindru care se rotește. Calculați aria suprafeței cilindrului rotativ.
Soluţie:
Raza cercului de bază este r= CD= a
Inaltimea cilindrului este h= OO'= AD=2a
Deci aria laterală a cilindrului este Sxq = 2πrh = 2π.a.2a =4a2π
Formula pentru calcularea ariei totale a unui cilindru
Suprafața totală este calculată ca mărime a întregului spațiu ocupat de figură, inclusiv aria laterală și aria celor două baze circulare.
Formula de calcul a ariei totale a unui cilindru este aria laterală plus aria celor două baze.
Exemplul 1 : Calculați aria totală a unui cilindru cu o bază de 3 și o înălțime de 5.
Soluţie:
Suprafața totală este Stp= Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π
Calculați înălțimea cilindrului
Înălțimea unui cilindru este distanța dintre cele două baze ale cilindrului.
Calculați înălțimea unui cilindru cunoscând suprafața totală și raza bazei
De exemplu: dat un cilindru cu raza bazei R = 8cm și aria totală 564π cm2 . Calculați înălțimea cilindrului.
Premiu:
Avem
Calculați înălțimea unui cilindru cunoscând aria laterală
=>
Formula pentru calcularea razei bazei unui cilindru
1. Formula de calcul a circumferinței unui cerc; zona cercului
Cercul are circumferința C=2πr
=>
Cercul cu baza are aria S=πr2
=>
De exemplu. Calculați raza bazei cilindrului în următoarele cazuri:
o. Circumferința cercului de bază este 6π
b. Aria bazei este de 25π
Soluţie:
o. Raza cercului de bază este
b. Raza cercului de bază este
2. Baza este cercul înscris în poligon
- Înscris în orice triunghi: cu S fiind aria triunghiului și p fiind semiperimetrul
- Înscris într-un triunghi echilateral: latura
- pătrat inscripționat:
Exemplul 1 . Având în vedere un cilindru înscris într-un cub cu muchia a. Calculați raza acelui cilindru.
Raza cilindrului este:
Exemplul 2 . Având în vedere o prismă regulată ABC.A'B'C' cu , volumul circumscris în jurul cilindrului. Calculați raza acelui cilindru.
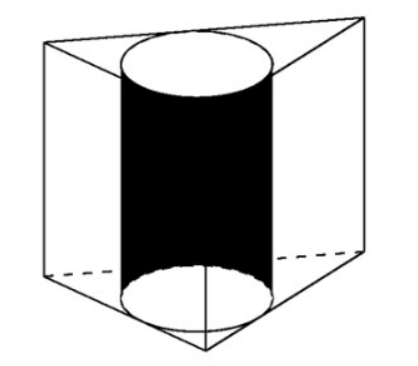
Volumul prismei este
Baza unei prisme regulate este un triunghi echilateral, deci => latura
Prin urmare, raza bazei cilindrului este:
3. Baza este cercul care circumscrie poligonul.
Circumscris în orice triunghi:
Acolo:
- a, b, c sunt lungimile celor trei laturi ale triunghiului
- p este semiperimetrul triunghiului:
Circumferința unui triunghi dreptunghic: ipotenuză
Periferia triunghiului echilateral: latura
Circumferința pătratului: latura
De exemplu:
Calculați raza bazei cilindrului care circumscrie piramida regulată S.ABC în următoarele cazuri:
o. ABC este un triunghi dreptunghic în A cu AB = a și AC = a√3
b. ABC are AB= 5; AC= 7; BC=8
Premiu:
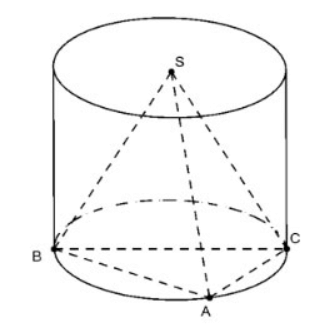
o. Ipotenuză
Deoarece ABC este un unghi drept la A, raza R=0,5.BC=a
b. Semiperimetrul triunghiului ABC este
Ce este un cilindru circular?
Un cilindru circular este un cilindru cu două baze circulare egale paralele între ele.
Cilindrii sunt folosiți destul de frecvent în probleme de geometrie de la bază la complexe, în care formula de calcul a ariei și volumului cilindrilor este adesea folosită diferit. Dacă știți deja cum să calculați aria și circumferința unui cerc, puteți deduce cu ușurință formulele pentru calcularea volumului, aria laterală și aria totală a unui cilindru.
Formula pentru calcularea ariei secțiunii transversale a unui cilindru
Tăiați cilindrul în plan (P) prin axă
- Secțiunea transversală rezultată este un dreptunghi.
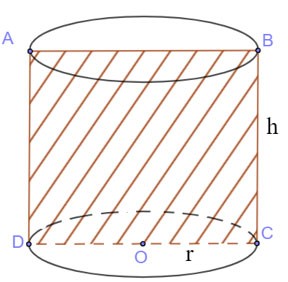 |
Aria secțiunii transversale:
SABCD = BC.CD =2r.h
|
Tăiați cilindrul în plan (P) paralel cu și la o distanță x de axă
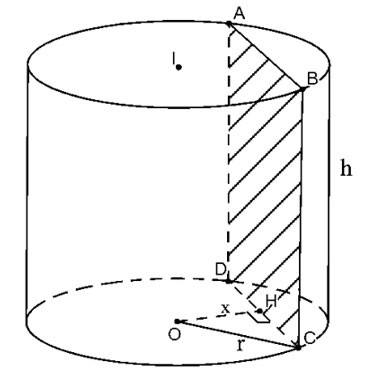 |
Secțiunea transversală rezultată este dreptunghi ABCD așa cum se arată mai sus.
Fie H mijlocul lui CD, avem OH ⊥ CD=>
Prin urmare aria secțiunii transversale
|
Tăiați cilindrul în plan (P) nu perpendicular pe axă, dar tăiați toate generatoarele cilindrului
 |
Secțiunea transversală formată este un cerc cu centrul O' și raza O'A'=r
Aria secțiunii transversale: S= πr2
|
Tăiați cilindrul în plan (P) nu perpendicular pe axă, dar tăiați toate generatoarele cilindrului.
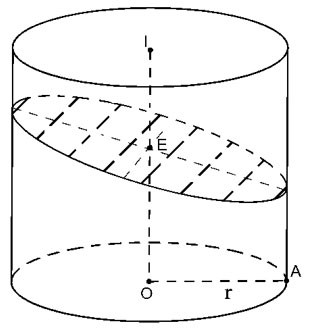 |
Secțiunea transversală rezultată este o elipsă (E) cu axa minoră 2r => a=r
Axa mare este egală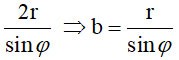
cu 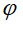 este unghiul dintre axa OI și (P) este unghiul dintre axa OI și (P)
Prin urmare aria S= π. ab=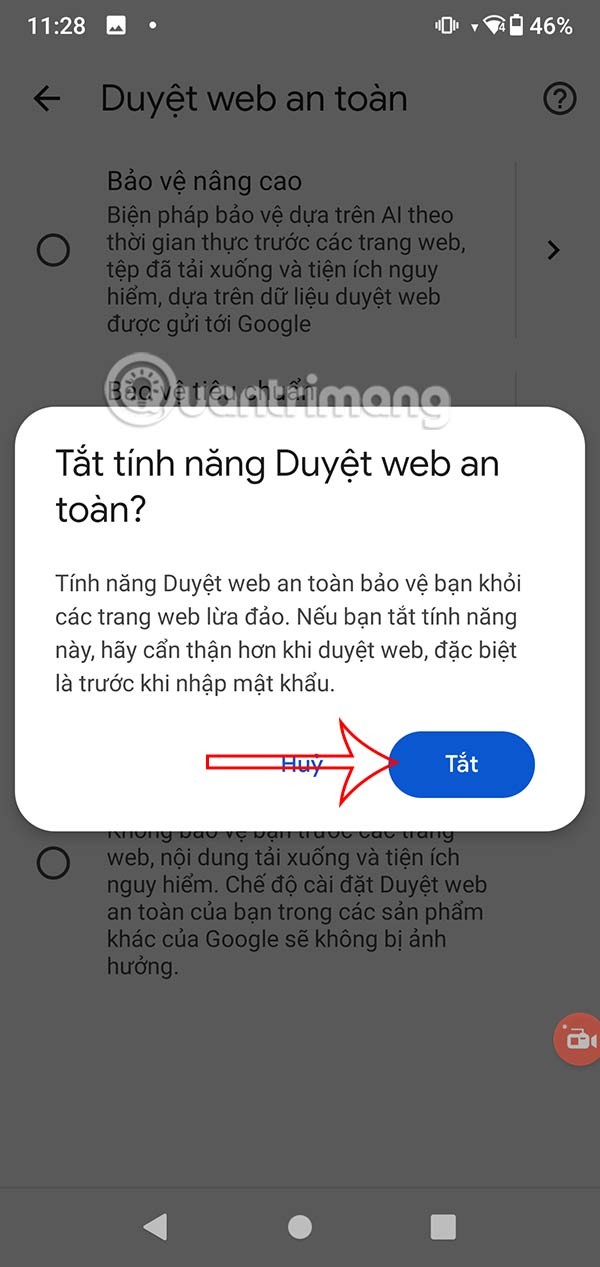
|
Exemplu de calcul al ariei unui cilindru
Lecția 1 :
Zona laterală a unui cilindru are o circumferință circulară a bazei de 13 cm și o înălțime de 3 cm.
Premiu:
Avem: circumferința cercului C = 2R.π = 13cm, h = 3cm
Deci aria laterală a cilindrului este:
Sxq = 2πr.h = Ch = 13,3 = 39 (cm²)
Lecția 2 : Având în vedere un cilindru cu raza cercului de bază de 6 cm, în timp ce înălțimea de la bază până la vârful cilindrului este de 8 cm grosime. Care este aria laterală și aria totală a cilindrului?
Premiu
După formula, avem semicercul de bază r = 6 cm și înălțimea cilindrului h = 8 cm. Prin urmare, avem formula pentru a calcula aria laterală a unui cilindru și aria totală a unui cilindru după cum urmează:
Aria suprafeței cilindrului = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 cm²
Aria totală a cilindrului = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²
Lecția 3 : Un cilindru are o rază de bază de 7 cm și o zonă laterală de 352 cm2.
Apoi, înălțimea cilindrului este:
(A) 3,2 cm; (B) 4,6 cm; (C) 1,8 cm
(D) 2,1 cm; (E) Un alt rezultat
Vă rugăm să selectați rezultatul corect.
Soluție: avem
Deci, răspunsul E este corect.
Lecția 4 : Înălțimea unui cilindru este egală cu raza cercului de bază. Suprafața laterală a cilindrului este de 314 cm2. Calculați raza cercului de bază și volumul cilindrului (rotunjiți rezultatul la două zecimale).
Premiu:
Suprafața laterală a cilindrului este de 314 cm2
Avem Sxq = 2.π.rh = 314
Unde r = h
Deci 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)
Volumul cilindrului: V = π.r2.h = π.r3 ≈ 1109,65 (cm³).
Sperăm că articolul de mai sus v-a ajutat să înțelegeți cunoștințele de bază și avansate despre cilindri, cum să calculați suprafața totală și aria laterală a unui cilindru.









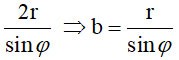
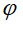 este unghiul dintre axa OI și (P)
este unghiul dintre axa OI și (P)