Ortocentrul unui triunghi este intersecția celor trei altitudini , adică intersecția liniilor de la fiecare vârf al triunghiului până la latura opusă formează un unghi drept. Lungimea altitudinii este distanța dintre partea de sus și de jos.
Ortocentrul unui triunghi
Cele trei altitudini ale unui triunghi se întâlnesc într-un punct. Acest punct se numește ortocentrul triunghiului .
Mai exact: În desen sunt înălțimile, ortocentrul triunghiului.
Pentru a determina ortocentrul unui triunghi, găsim intersecția celor două altitudini din acel triunghi.
Notă: a) Dacă triunghiul este un triunghi ascuțit, ortocentrul se află în interiorul triunghiului.
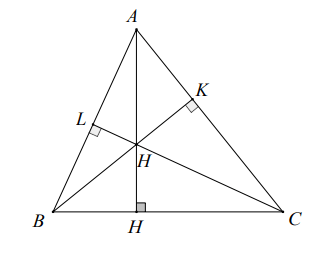
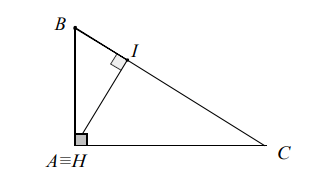
b) Dacă triunghiul este un triunghi dreptunghic la atunci ortocentrul coincide cu punctul .
c) Dacă un triunghi este un triunghi obtuz, atunci ortocentrul se află în afara triunghiului.
Proprietatea 1: Într-un triunghi echilateral, centroidul, ortocentrul, un punct echidistant de cele trei vârfuri ale triunghiului, un punct în interiorul triunghiului și echidistant de cele trei laturi ale triunghiului sunt patru puncte coincidente.
Proprietatea 2: Ortocentrul taie bisectoarea perpendiculară a două laturi în două segmente de lungime egală. Aceasta înseamnă că ortocentrul este la aceeași distanță de vârfurile triunghiului.
Proprietatea 3: Ortocentrul este centrul cercului circumferitor al unui triunghi, adică dacă desenăm un cerc care trece prin cele trei vârfuri ale unui triunghi, ortocentrul va fi centrul acelui cerc.
Proprietatea 4: Ortocentrul unui triunghi acut se află în interiorul triunghiului, în timp ce ortocentrul unui triunghi obtuz se află în afara triunghiului.
Proprietatea 5: Ortocentrul unui triunghi dreptunghic coincide cu vârful unghiului drept al acelui triunghi dreptunghic.
Proprietatea 6: Ortocentrul este singurul punct dintr-un triunghi, astfel încât dacă trasăm linii de la ortocentru la vârfurile triunghiului, suma lungimilor acelor linii este cea mai mică. Aceasta înseamnă că ortocentrul este cel mai aproape de vârfurile triunghiului decât orice alt punct.
Proprietatea 7: Ortocentrul este și centrul cercului circumferitor al triunghiului, adică cel mai mare cerc care poate fi trasat prin cele trei vârfuri ale triunghiului.
De exemplu: dat non-pătrat. Sună-i ortocentrul. Arată înălțimile triunghiului. De acolo, indicați ortocentrul acelui triunghi.
Ghid de soluții
Ilustrare
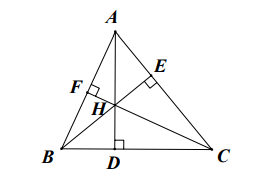
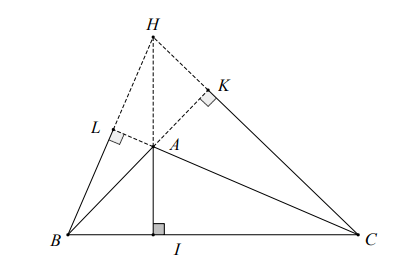
Fie picioarele perpendicularelor trase din ΔABC.
Luați în considerare ΔHBC cu:
deci AD este înălțimea de la H la BC.
la F deci BA este altitudinea de la B la HC
la E deci CA este înălțimea de la C la HB.
se intersectează la A deci A este ortocentrul lui ΔHCB.
De exemplu: dat un triunghi dreptunghic cu înălțimea . Fie punctul de mijloc al fie , punctul de mijloc al este . Determinați ortocentrul triunghiului.
Ghid de soluții
Luați în considerare sub-problema dacă triunghiul are și AC ca puncte de mijloc, respectiv, atunci și .
Într-adevăr, pe raza opusă a razei ia un punct astfel încât
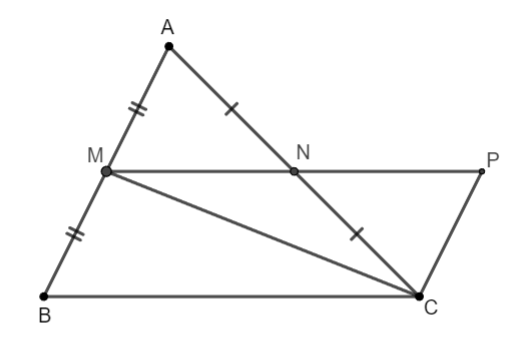
Luați în considerare triunghiul AMN și triunghiul CPN.
(opus)
, (două laturi și două unghiuri corespunzătoare)
Două unghiuri sunt în poziții alternative deci
=>(două unghiuri interioare alternative)
Luați în considerare triunghiul BMC și triunghiul PCM.
(cmt)
MC este o margine comună
, (laturile și unghiurile corespunzătoare)
Două unghiuri sunt în poziții alternative deci
Avem din nou
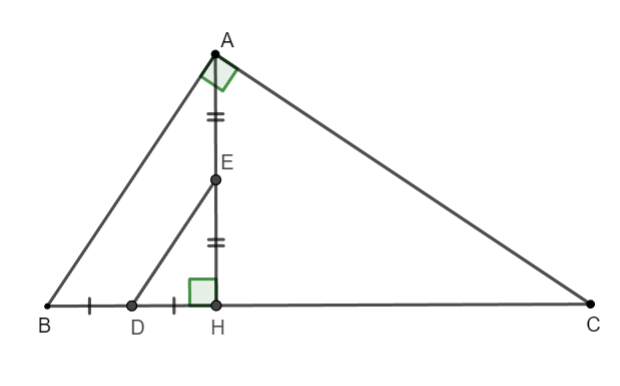
Luați în considerare triunghiul HAB cu:
(după cum s-a dovedit mai sus)
Luați în considerare triunghiul ADE.
pe de altă parte şi
este înălțimea triunghiului ADE
C este intersecția dintre AC și DC
=> C este ortocentrul triunghiului ADE
De exemplu: Având în vedere o scară la A, altitudinea intersectează mediana la . Demonstrați și calculați?
Instrui
Ilustrare
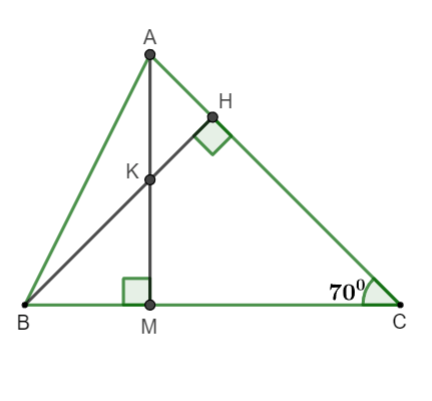
Pentru că soldul este la A și AM este mediana
⇒ AM este și altitudinea corespunzătoare lui BC
la M.
Pe de altă parte, și deci K este ortocentrul.
Prin urmare, K aparține altitudinii de la C a lui ∆ABC.
Avem:
Compară activități secundare realiste pentru 2026 în funcție de costul de pornire, comisioane, flexibilitate și controlul veniturilor, cu îndrumări actuale privind impozitele și escrocheriile din surse oficiale.
Îmbunătățiți-vă ergonomia biroului de acasă cu îndrumările OSHA și NIOSH actuale privind potrivirea scaunului, înălțimea monitorului, configurarea laptopului, iluminarea și mișcarea.
Află de ce contează inteligența emoțională în leadership, unde ajută cel mai mult, cum să o consolidezi și cum să-ți dai seama dacă abordarea ta funcționează.
O foaie de parcurs practică pentru a intra în domeniul tehnologiei fără diplomă: alege un rol accesibil, dezvoltă abilități pregătite pentru angajare, demonstrează-le prin proiecte și folosește feedback-ul de la angajare pentru a te îmbunătăți.
Build a credible LinkedIn personal brand in 2026 with current profile, content, newsletter, analytics, verification, and visibility guidance from LinkedIn.
Demisiile discrete și concedierile discrete sunt etichete atrăgătoare, nu diagnostice. Aflați ce se verifică, ce depinde de context și ce pot face angajații și managerii în continuare.
Directorii executivi fracționari oferă funcții de conducere fără angajare cu normă întreagă. Învață când funcționează modelul, ce să ceri și riscurile de gestionat.
Pregătiți o cerere de mărire salarială mai convingătoare pentru trimestrul 4, incluzând date salariale actuale, opțiuni de sincronizare, compromisuri salariale și scenarii pentru rezultate afirmative, parțiale sau negative.
Choose a high-income skill you can realistically start before 2026 ends, with current pay data, learning priorities, and a practical self-check.
Construiește un program de lucru hibrid în jurul sarcinilor, suprapunerii echipei și rezultatelor măsurabile. Vezi modele, semne de avertizare și când să-ți ajustezi planul.
