Ce este un număr rațional? Ce este un număr irațional?

Definițiile și formulele numerelor raționale și iraționale sunt cunoștințe importante în matematică pe care elevii trebuie să le înțeleagă pentru a avea o bază matematică solidă. Următorul articol vă prezintă definiția, proprietățile și formele matematice ale numerelor raționale și iraționale. Vă rugăm să consultați el.

Numere raționale, numere iraționale

• Ce este un număr rațional?
  • Clasificarea numerelor raționale
  • Reprezentarea numerelor raționale pe o dreaptă numerică
  • Adunarea și scăderea numerelor raționale
  • Înmulțirea și împărțirea numerelor raționale
  • Valoarea absolută a unui număr rațional
  • Comparați două numere raționale
  • Formula pentru calcularea puterii unui număr rațional
• Ce este un număr irațional?
  • Conceptul de numere iraționale
  • Proprietățile numerelor iraționale
• Care este diferența dintre numerele raționale și iraționale?
• Relația dintre mulțimi de numere
• Exerciții pe numere raționale

Ce este un număr rațional?

- Numerele raționale sunt mulțimea numerelor care pot fi scrise ca fracții (coeficienti). Adică, un număr rațional poate fi reprezentat printr-o zecimală recurentă infinită.

- Numerele raționale sunt scrise ca , unde a și b sunt numere întregi, dar b trebuie să fie diferit de 0.

- este mulţimea numerelor raţionale.

=> Mulțimea numerelor raționale: .

De exemplu: , , … sunt numere raționale.

• Orice număr întreg a este un număr rațional deoarece întregul a poate fi scris sub forma .

De exemplu: Avem numere raționale.

Avem:

Comentariu: toate sunt numere raționale.

Clasificarea numerelor raționale

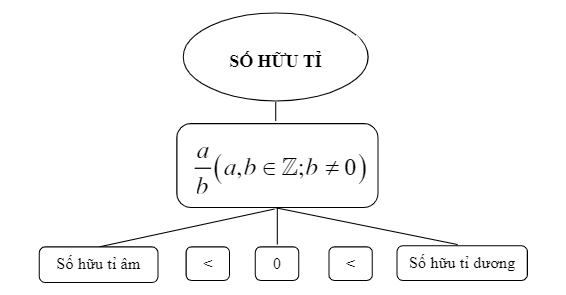
Numerele raționale sunt împărțite în două tipuri: numere raționale negative și numere raționale pozitive. Mai exact:

• Numere raționale negative: includeți numere raționale mai mici decât 0.
• Numere raționale pozitive: includeți numere raționale mai mari decât 0.

Notă: numărul 0 nu este nici un număr rațional negativ, nici un număr rațional pozitiv.

Natură

• Mulțimea numerelor raționale este o mulțime numărabilă.
• Proprietate comutativă:
• Proprietate de adunare cu 0:
• Proprietăți combinate:

Reprezentarea numerelor raționale pe o dreaptă numerică

- Pentru a reprezenta numerele raționale pe dreapta numerică, urmărim acești factori:

Pasul 1: Scrieți numărul rațional sub formă de fracție

Pasul 2: Împărțiți segmentul de linie unitară în b părți egale pentru a obține un nou segment de unitate care este vechea unitate.

Pasul 3: Numărul rațional este reprezentat de punctul A fiind o distanță de unități noi față de punctul 0.

• A este la stânga lui 0 dacă este un număr negativ.
• A este la dreapta lui 0 dacă este un număr pozitiv.

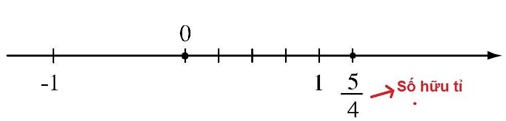
De exemplu: În figură, punctul P reprezintă numărul rațional:

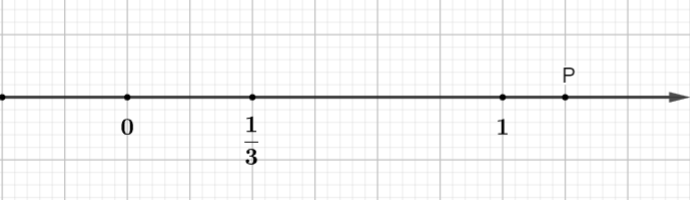
Instrui

Segmentul de linie al unității este împărțit în 6 părți egale (unitatea nouă este 1/6 din unitatea veche)

Punctul P este situat la o distanță de 7 noi unități de punctul O.

Și punctul P este la dreapta punctului O, deci P este un număr rațional pozitiv.

Deci P reprezintă un număr rațional.

Adunarea și scăderea numerelor raționale

i) Reguli de adunare și scădere a două numere raționale

Putem aduna și scădea două numere raționale x și y scriindu-le ca două fracții și apoi aplicând regulile de adunare și scădere a fracțiilor.

La noi avem:

ii) Proprietăți

- Adunarea numerelor raționale are proprietăți de adunare a fracțiilor: comutativă, asociativă, adunare cu 0, adunare cu contrarii.

- Avem:

a) Proprietatea comutativă:

b) Proprietăți asociative:

c) Adăugați 0:

d) Adăugați numărul opus:

iii, Reguli de tranziție

Când mutam un termen dintr-o parte a unei ecuații în cealaltă, trebuie să schimbăm semnul acelui termen.

În Q avem o sumă algebrică, în care putem schimba termeni, pune paranteze pentru a grupa în mod arbitrar termenii ca sumele algebrice din mulțimea numerelor întregi.

• Cu dacă atunci
• La noi avem:

Înmulțirea și împărțirea numerelor raționale

i) Reguli pentru înmulțirea și împărțirea a două numere raționale

- Putem înmulți și împărți două numere raționale scriindu-le ca fracții și apoi aplicând regulile de înmulțire și împărțire a fracțiilor.

• La noi avem:
• La noi avem:

De exemplu:

Înmulțirea numerelor raționale: 

Împărțirea numerelor raționale: 

ii) Proprietăți

- Înmulțirea numerelor raționale are, de asemenea, aceleași proprietăți ca și înmulțirea fracțiilor: comutativă, asociativă, înmulțire cu 1 și proprietate distributivă a înmulțirii peste adunare.

- Fiecare număr rațional diferit de zero are un invers.

- Avem:

• Proprietate comutativă: .
• Proprietăţi asociative: .
• Proprietatea înmulțirii cu 1: .
• Proprietăți distributive: .
• Cu . Reciproca lui a este .

Valoarea absolută a unui număr rațional

- Valoarea absolută a unui număr rațional a, notat cu , este distanța de la punctul a la punctul 0 pe dreapta numerică.

De exemplu:

(Pentru ca)

(Pentru ca)

Comparați două numere raționale

- Cu oricare 2 numere raționale avem întotdeauna fie sau sau .

- Pentru a compara două numere raționale facem următoarele:

• Scrieți sub formă de 2 fracții cu același numitor pozitiv:
• Comparați numărătorii ca numere întregi a, b:

De exemplu: Comparați două numere raționale: și

Avem:

Pentru că este bine.

Formula pentru calcularea puterii unui număr rațional

Formule pentru calcularea puterilor numerelor raționale pe care trebuie să le amintiți

• Produsul a două puteri cu aceeași bază:
• Puterea puterii
• Puterea unui produs
• Puterea unui coeficient

Ce este un număr irațional?

Conceptul de numere iraționale

• Când se menționează numere raționale, nu se poate să nu menționeze numere iraționale. Acestea sunt numere scrise sub formă de zecimale infinite, care nu se repetă, notate cu .
• Numerele reale care nu sunt numere raționale nu pot fi reprezentate ca rapoarte.

De exemplu: 3,145248... este un număr irațional.

Proprietățile numerelor iraționale

Mulțimea numerelor iraționale este o mulțime nenumărabilă.

De exemplu:

Numere iraționale: 0,1010010001000010000010000001... (aceasta este o zecimală infinită care nu se repetă)

Număr de rădăcini pătrate: √2 (rădăcină pătrată)

Pi (π): 3,14159 26535 89793 23846 26433 83279 50 288...

Care este diferența dintre numerele raționale și iraționale?

• Numerele raționale includ zecimale recurente care nu se încheie, în timp ce numerele iraționale sunt zecimale care nu se repetă.
• Numerele raționale sunt doar fracții, în timp ce numerele iraționale au multe tipuri diferite de numere.
• Numerele raționale sunt numere numărabile, în timp ce numerele iraționale sunt numere nenumărabile.

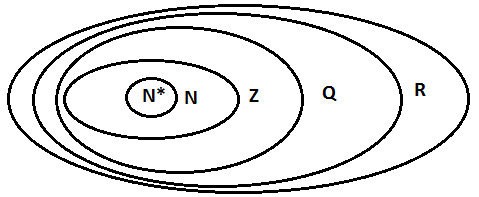
Relația dintre mulțimi de numere

Simboluri ale setului de numere:

• N: Set de numere naturale
• N*: set de numere naturale altele decât 0
• Z: set de numere întregi
• Î: Mulțimea numerelor raționale
• I: Set de numere iraționale

Avem: R = Q ∪ I.

Setul N; Z; Q; R.

Atunci relația de includere dintre mulțimile de numere este: N ⊂ Z ⊂ Q ⊂ R

Exerciții pe numere raționale

Forma 1: Efectuați calcule care implică numere raționale

Metoda de rezolvare: Pentru a rezolva exerciții privind efectuarea de calcule legate de numerele raționale, mai întâi convertiți numerele raționale în fracții, apoi aplicați regulile de calcul cu adunarea, scăderea, înmulțirea și împărțirea numerelor raționale.

Exemplu: Calculați  

Răspuns:

Forma 2: Reprezentarea numerelor raționale pe linia numerică

Soluție: Trebuie să determinați dacă numărul rațional este un număr rațional pozitiv sau un număr rațional negativ, apoi continuați cu următorii pași:

• Dacă numărul rațional a/b este un număr rațional pozitiv: Pe linia numerică, în direcția pozitivă, împărțiți lungimea unei unități în b părți egale. Apoi luați un punct pe direcția pozitivă a axei Ox, punctați o parte și determinați poziția numărului rațional a/b.
• Dacă numărul rațional a/b este un număr rațional negativ: Pe dreapta numerelor, în direcția negativă a axei, împărțiți lungimea unei unități în b părți egale. Apoi luați un punct pe direcția negativă a axei Ox, punctați o parte și determinați poziția numărului rațional a/b.

Forma 3: Compararea numerelor raționale

Soluție: Transformați numerele raționale date în fracții cu același numitor pozitiv, apoi comparați numărătorii. Mai avansate putem compara cu fracțiile intermediare pentru a găsi răspunsul.

Forma 4: Stabiliți dacă un număr rațional este negativ, pozitiv sau 0

Metoda de rezolvare: Pentru a rezolva exercițiile de tip 4, elevii trebuie să se bazeze pe proprietățile numerelor raționale pentru a determina dacă numărul rațional este negativ, pozitiv sau 0.

De exemplu: Având în vedere numărul rațional x = (a – 25)/29, determinați valoarea lui a astfel încât:

• x este negativ
• x este pozitiv
• x = 0

Răspuns:

x este un număr negativ => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x este un număr pozitiv => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 =0 0 => a – 25 = 0 => a = 25

Forma 5: Găsiți numere raționale în interval în funcție de condițiile date

Soluție: Dacă întrebarea necesită găsirea numerelor raționale într-un interval în conformitate cu condițiile date, trebuie să punem numerele raționale în același numărător sau numitor pentru a găsi răspunsul.

Exemplu: Găsiți valoarea lui m pentru mai mare decât și mai mic decât

Ghid de răspunsuri

Convertiți fracțiile în numitori comuni după cum urmează:

Numitor comun: 18

Dupa intrebare avem:

Forma 6: Găsiți x cu numere raționale

Metodă de rezolvare a problemelor de matematică: Pentru ca problemele de matematică să găsească x cu numere raționale, este necesar să se efectueze reducerea la numitor comun și să se transforme x într-o parte, iar termenii rămași la 1. De acolo se calculează valoarea lui x

De exemplu: Găsiți x cunoscând x . (2/ 3) + 5/ 6 = 1/ 8

Răspuns:

x . (2/ 3) + 5/ 6 = 1/ 8

=> x . (2/ 3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Forma 7: Găsiți a astfel încât expresia să fie un număr întreg

Metoda de rezolvare a problemelor de matematică: Pentru problema găsirii a, dacă numărătorul nu conține a, trebuie să folosim semnul de divizibilitate. Dacă numărătorul conține a, utilizați semnul de divizibilitate sau separați numărătorul după numitor. Dacă problema necesită găsirea ambelor a și b în același timp, grupați a sau b și convertiți-le în formă fracțională pentru calcul.

Exemplu: Găsiți numărul întreg a cu condiția ca 8/(a – 1) să fie un număr întreg

Răspuns:

Condiție: a – 1 ≠ 0 => a ≠ 1

Fie a un număr întreg => 8 este divizibil cu (a – 1)

=> (a – 1) este un factor de 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Sperăm că articolul de mai sus v-a ajutat să înțelegeți ce sunt numerele raționale, ce sunt numerele iraționale, tipurile de numere raționale, ce sunt simbolurile numerelor raționale și cum să recunoașteți numerele raționale pentru a rezolva cu ușurință probleme.

Pe lângă cunoștințele despre numerele iraționale și numerele raționale de mai sus, vă puteți referi la alte cunoștințe matematice, cum ar fi fracții , numere mixte , zecimale ...