Ce sunt numerele reale? Ce numere sunt în mulțimea numerelor reale? Vă rugăm să citiți articolul de mai jos pentru a înțelege mai bine aceste importante cunoștințe matematice.
Număr real
1. Ce este un număr real?
- Numerele reale sunt mulțimea numerelor raționale și a numerelor iraționale.
- Mulțimea este simbolul pentru mulțimea numerelor reale, constând din numere reale.
- Un număr rațional este un număr scris ca o fracție (a, b ∈ Z, b ≠ 0). De exemplu
- Mulțimea numerelor raționale se notează cu
- Un număr irațional este o zecimală infinită, care nu se repetă. De exemplu:
- Mulțimea numerelor iraționale se notează cu
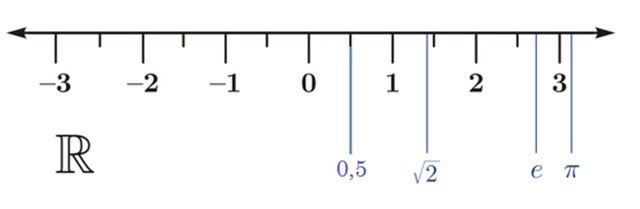
Setul de numere reale acoperă linia numerică.
De exemplu:
2. Axa numerelor reale
Fiecare număr real este reprezentat de un punct pe dreapta numerelor.
- Invers, fiecare punct de pe dreapta numerică reprezintă un număr real.
- Numai mulțimea de numere reale umple linia numerică.
3. Comparați numerele reale
Metodă
- Cu oricare două numere reale x, y avem întotdeauna x = y sau x < y sau x > y
- Numerele reale mai mari decât 0 se numesc numere reale pozitive, numerele reale mai mici decât 1 se numesc numere reale negative. Numărul 0 nu este un număr real nici pozitiv, nici negativ.
- Compararea numerelor reale pozitive este similară cu compararea numerelor raționale.
- Cu a, b fiind două numere reale pozitive, dacă a > b atunci .
Exemplu: completați cifra corespunzătoare în pătrat:
| a) -7,5(...)8 > -7,513 |
b) -3,02 <> |
| c) -0,4(...)854 <> |
d) -1,(...)0765 <> |
Ghid de soluții
a) -7,5(0)8 > -7,513
b) -3,02 <>
c) -0,4(9)854 <>
d) -1,(9)0765 <>
Exemplu: Aranjați numerele reale: în ordine de la cel mai mic la cel mai mare
Ghid de soluții
Aranjați numerele reale în ordine de la cel mai mic la cel mai mare:
De exemplu: Demonstrați că:
Cu a, b sunt două numere reale pozitive dacă a > b atunci
Ghid de soluții
Dacă a > b atunci
a, b sunt două numere reale pozitive, deci a + b > 0
Dacă a > b atunci a – b > 0
Luați în considerare produsul
Deoarece a2 – b2 > 0
=> a2 > b2 => dpcm
3. Proprietăţile mulţimii numerelor reale
În mulțime, definim și operațiile de adunare, scădere, înmulțire, împărțire, exponențiere, rădăcini pătrate... Iar în operații, numerele reale au și ele aceleași proprietăți ca și operațiile din mulțimea numerelor raționale.
În mulțimea numerelor reale, operațiile au următoarele proprietăți în ceea ce privește înmulțirea:
- Pentru toate proprietățile:
- Adăugați 0:
- Proprietate comutativă: ;
- Proprietăți combinate:
- Proprietatea comutativă: a. b = b. o
- Proprietăţi asociative: (a. b). c = a. (b. c)
- Proprietățile înmulțirii cu numărul 1:
- Proprietatea distributivă a înmulțirii peste adunare: a. (b + c) = a. b + a. c
- Pentru fiecare număr real a ≠ 0, există o inversă astfel încât
- Adică calculele de mai sus au și proprietăți comutative și asociative ca și alte seturi de numere. Și același lucru este valabil și pentru scăderea, înmulțirea, împărțirea...
Relația dintre seturile de numere
De exemplu: Efectuați calculul:
Ghid de soluții
De exemplu: Găsiți x, știind:
Ghid de soluții
4. Valoarea absolută a unui număr real
Definiție: Distanța de la punctul a la punctul 0 pe linia numerică este valoarea absolută a unui număr a (a este un număr real). Valoarea absolută a unui număr negativ este însăși, valoarea absolută a unui număr negativ este opusul său.
Prezentare generală:
Natură
- Valoarea absolută a fiecărui număr este nenegativă.
- General: pentru toate a ∈ R
Mai exact:
Unele proprietăți
- Două numere care sunt egale sau opuse au valoare absolută egală și invers, două numere care au valoare absolută egală sunt egale sau opuse.
Prezentare generală:
- Fiecare număr este mai mare sau egal cu opusul valorii sale absolute și, în același timp, mai mic sau egal cu valoarea sa absolută.
Prezentare generală: și
- Dintre două numere negative, cel mai mic are valoarea absolută mai mare.
Prezentare generală: Dacă
- Dintre două numere pozitive, cel mai mic are valoarea absolută mai mică.
Prezentare generală: Dacă
- Valoarea absolută a unui produs este egală cu produsul valorilor absolute.
Prezentare generală:
- Valoarea absolută a unui coeficient este egală cu câtul a două valori absolute.
Prezentare generală:
5. Exemple de exerciții pe numere reale
Exemplul 1: Completați spațiile libere cu simbolurile adecvate ∈, ∉, ⊂ (…):
3 …. Q; 3 …. R; 3… eu ; -2,53... Q;
0.2(35) …. eu ; N…. Z; eu…. R.
Instrui
a) 3 ∈ Q ; 3 ∈ R ; 3 ∉ I ; -2,53 ∈ Q
b) 0,2(35) ∉ I ; N ∈ Z ; eu ⊂ R
Exemplul 2: Găsiți seturile
a) Q ∩ I ;
b) R ∩ I.
Instrui
a) Q ∩ I = Ø ;
b) R ∩ I = I.
Exemplul 3: completați cifra corespunzătoare în (...)
a) – 3,02 < –="" 3,="" …="">
b) – 7,5 … 8 > – 7,513
c) – 0,4 … 854 < –="">
d) -1, … 0765 < –="">
Instrui
a) – 3,02 < –="">
b) – 7.508 > – 7.513 ;
c) – 0,49854 < –="" 0,49826="">
d) -1,90765 < –="">
Exemplul 4: Găsiți x, știind:
3.2.x + (-1.2).x +2.7 = -4.9;
Instrui
3.2. x + (-1,2).x + 2,7 = -4,9
[3,2 + (-1,2)].x + 2,7 = -4,9.
2.x + 2.7 = – 4.9.
2.x = – 4,9 – 2,7
2.x = – 7,6
x = -7,6 : 2
x = -3,8
Pe lângă numerele reale, puteți afla mai multe despre alte definiții din matematică, cum ar fi numere pătrate , numere iraționale, numere raționale , numere prime , numere naturale ...